参考链接🔗:
https://zhuanlan.zhihu.com/p/614115887
https://bbs.scumaker.org/t/topic/560
https://www.bilibili.com/video/BV1iz421h7gb/?spm_id_from=333.337.search-card.all.click&vd_source=afa3ea0b45313227b053b5fa593eccaa
本文概览
这篇博客的目的不只是学习记录——PPO是怎么样的?GRPO又是如何沿着PPO设计得到的?
当我试图了解上面两个问题的时候,我看了一些文章和视频,并开始认为:“单纯地学一个东西本身,是无法把这个东西学明白的”,你只能知道这个东西是什么,怎么用,但是无法学到这个东西内在蕴含的智慧。我觉得如果有时间,可以采取一种更好的学习模式如下:
这个东西背后的历史:它是怎么来的。
从数学(万物的操控者)的角度看这个东西,它是怎么样的。
从使用(程序员)的角度看这个东西,它是怎么样的。
从直觉来看,它是怎么样的。
我决定按照这样的思路来介绍PPO和GRPO。
PPO怎么来的
该部分主要参考:https://zhuanlan.zhihu.com/p/614115887
简单回顾下强化学习
之前在“探索和利用”博客里面介绍过最简单的强化学习Q-learning。
Q-learning就是我们有一个智能体,这个智能体通过和环境的交互,也就是在所有状态下,执行所有可能的动作;在这个过程中,它不断更新在某状态下做出某个动作会得到的回报值。
这是“基于值函数”的强化学习,就是它通过一个动作价值函数,通常表示为Q(s, a),计算在状态s下采取动作a所期望获得的累积回报,从而指导智能体的动作选择。这样的强化学习,一旦学到了固定的动作价值函数Q,之后在每个状态采取的动作就是固定的了。
后面,改了,大部分的强化学习算法使用基于策略的方式:
不再通过价值函数来确定选择动作的策略,而是直接学习策略本身,通过一组参数 θ 对策略进行参数化,并通过神经网络方法优化 θ 。
具体来说,基于策略的方式不学习“动作的价值”了,而是学习某个状态下采取各个动作的概率,在返回的动作概率列表中对不同的动作进行抽样选择。(有助于实现探索的多样性)
策略梯度到自然梯度
基于策略的方式是如何工作的呢?
首先最重要的是目标函数和参数对函数的梯度:


根据这个思路,就有了REINFORCE算法,经典的策略梯度算法之一:


0. 输入:
- 初始化参数θ,这些参数是策略的参数。
1. 循环:for n=1 to N do
- 进行 N 次迭代。
2. 生成轨迹:
- 使用当前策略 π(生成一个状态-动作轨迹tau。
3. 计算累积奖励:for t=1 to T do
- 对于轨迹中的每个时间步 t,计算从时间步t到终止状态的累积奖励。
4. 计算累积奖励:
- 计算从时间步t开始的累积奖励。
5. 更新参数:
- 使用梯度上升方法更新参数θ,其中α是学习率,∇_θ x xlog(π_θ(a | s))是策略的梯度
那么,由着策略梯度算法,人们又是如何发明出自然梯度算法的呢?(大佬写的好,直接复制来)其实是受到一个有趣的现象的启发:
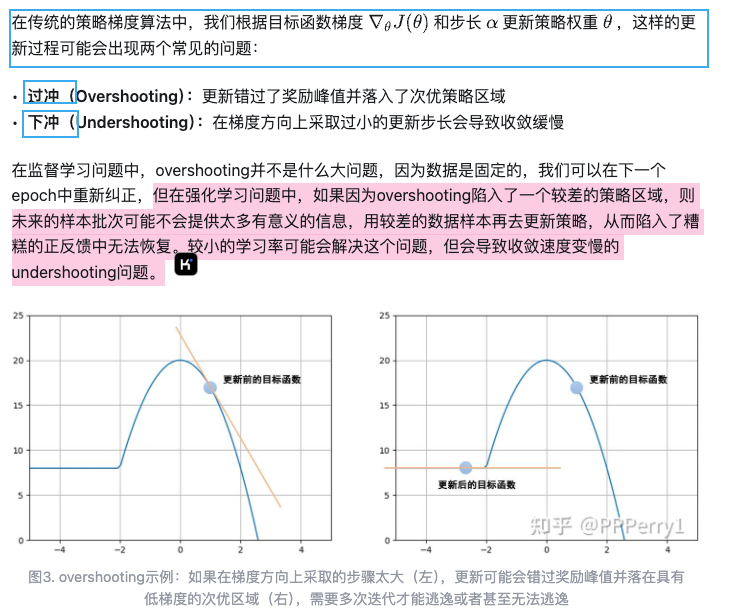
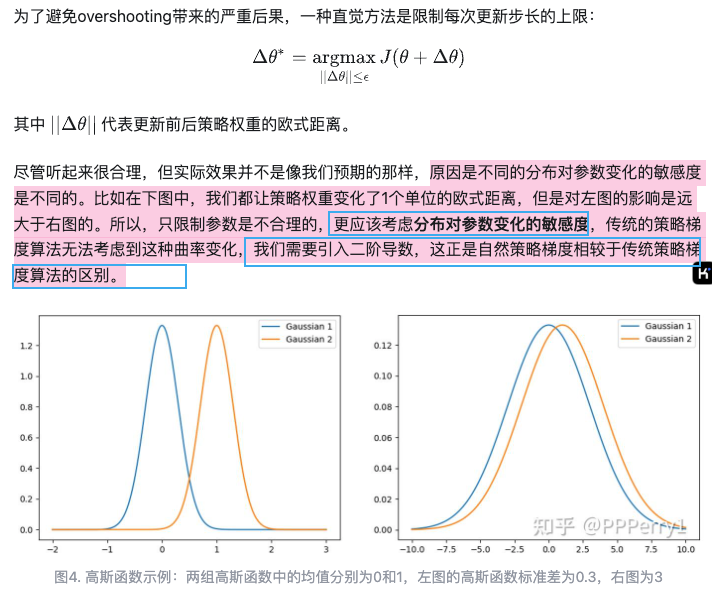
下面是自然梯度的数学原理(哎,好厉害,推动算法的历史进程往前走的东西,根本上还是数学吧):

前面还有一堆数学推导,感兴趣自己看原文哦

好的然后来看下伪代码:

收集轨迹:在当前策略 πk=π(θk) 下,收集一组轨迹 Dk。这些轨迹包含了在环境中执行策略时的状态、动作和奖励序列。
估计优势函数:使用任意优势估计算法估计优势函数 A^tπk。优势函数衡量在特定状态下采取某个动作相对于平均情况的好坏。
形成样本估计:
策略梯度 g^k:使用优势估计来计算策略梯度的样本估计。
KL散度Hessian / Fisher信息矩阵 Hk:计算KL散度的Hessian矩阵或Fisher信息矩阵的样本估计。这些矩阵用于调整策略更新的方向和步长,以提高学习效率。
计算自然策略梯度更新
更新策略参数 θk+1
自然梯度到信赖域策略优化(TRPO)算法
自然策略梯度算法的缺陷:
近似值可能会违反KL约束,从而导致分析得出的步长过大,超出限制要求;
矩阵𝐹−1的计算时间太长,是𝑂(𝑁3)复杂度的运算;
我们没有检查更新是否真的改进了策略。由于存在大量的近似过程,策略可能并没有优化。

在实际的算法实现方面,TRPO和自然策略梯度算法没有太大的区别。TRPO主要有三个改进,每个改进都解决了原始算法中的一个问题。TRPO的核心是利用单调改进定理,验证更新是否真正改进了我们的策略。
如果有更多的耐心了解TRPO的数学机制的话,它通过以下几个方面改进来自然梯度算法。
引入共轭梯度法避免逆Fisher矩阵的计算。
为了确保策略更新满足KL散度约束,采用了线搜索的方法来调整更新步长,从而保证了策略更新的稳定性和有效性。
在 TRPO中,我们并没有直接假设策略更新后会提高替代优势函数L(θ),而是通过实际的计算来真正验证这一点。虽然在实际计算过程中,需要依据旧策略来计算优势,并且利用重要性抽样来调整概率,这会耗费一定的时间,但为了确保策略更新确实能够带来改进,进行这样的验证是很有必要的。
TRPO到PPO
TRPO算法解决了许多与自然策略梯度相关的问题,并获得了RL社区的广泛采用。但是,TRPO仍然存在一些缺点,特别是:
无法处理大参数矩阵:尽管使用了共轭梯度法,TRPO仍然难以处理大的 Fisher矩阵,即使它们不需要求逆
二阶优化很慢:TRPO的实际实现是基于约束的,需要计算上述Fisher矩阵,这大大减慢了更新过程。此外,我们不能利用一阶随机梯度优化器,例如ADAM
TRPO 很复杂:TRPO很难解释、实现和调试。当训练没有产生预期的结果时,确定如何提高性能可能会很麻烦
在TRPO的基础上,Schulman等人引入了近端策略优化算法PPO(Proximal Policy Optimization)。有两种主要的PPO变体需要讨论(均在17年的论文中介绍):PPO Penalty和PPO Clip。
在TRPO里面,引入了一个“与KL散度相乘的惩罚项”,从而试图在策略更新时控制新策略与旧策略之间的差异,避免策略更新过大导致的不稳定。

因为是基于惩罚项的(如果超过了目标分布,就进行惩罚),所以叫做PPO Penalty算法。


小结:直觉上来说就是一句话
前面说了不少,原文里也有很多内容,但其实,从策略梯度发展到PPO,算法的每一步发展都是为了“更好地控制智能体的步长”,防止智能体学到的策略-奖励分布与实际的策略-奖励分布相差太大,避免它“走弯路”。
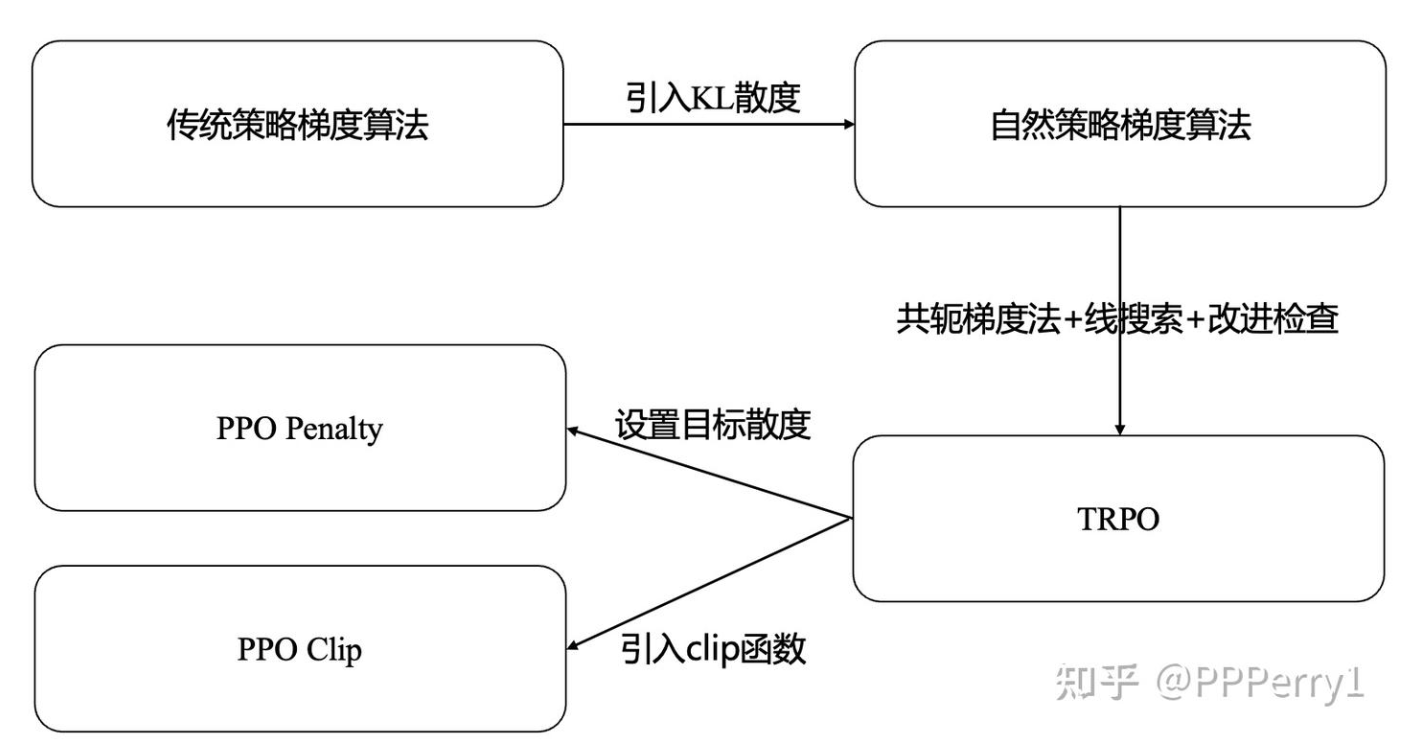
画个图,那么强化学习算法发展的脉络,大概就是如此:
PPO具体是怎么样的
上一部分咱们其实是从直觉上看了下PPO到底怎么来的,但是我们还没深入PPO的细节,比如,它是如何优化神经网络的(损失函数),它在代码里是如何工作的。
PPO:从损失函数入手
先让我们看下面左栏,看看损失函数是什么样子。上面一张图先后显示了PPO-Penalty和PPO-Clip的损失函数,它们的区别在于:
首先
P_θ和P_θ‘分别代表智能体学习的策略和参考策略,它们的比值反映了学习策略的分布对参考概率分布的偏离程度
PPO-Clip使用截断的方式。“clip():”里面的内容表示,如果这个程度在
[1-ε,1+ε]之间,那就取原来的值,如果小于区间就取区间下界,大于区间就取区间上界。相比于PPO-Penalty,这种设置更加方便。
PPO-Penalty则是为KL散度设置了一个缩放因子β (具体作用见上一部分)。
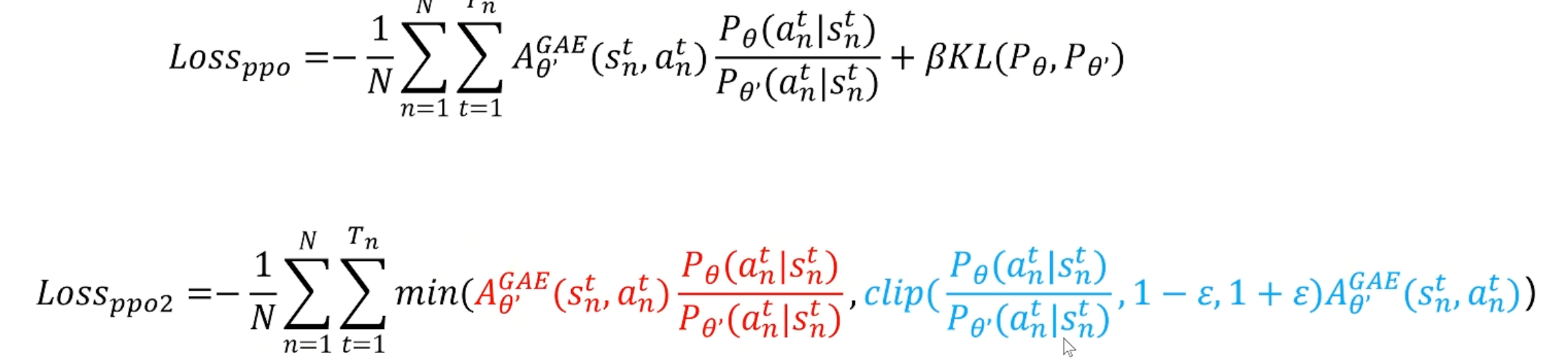



在知道A_θ^GAE是什么之前,可以先看看A_θ是什么(上面右图):
在原始的策略梯度中,回报使用(R_t^n - B(S_n^t)来计算,表示智能体采取的动作相比baseline模型有了多大的改进,然后乘以概率求期望。但是R_t^n 的获取来源于随机采样,不太稳定,所以人们引入传统的动作价值函数Q_θ,来计算采取某个动作,优势有多大。
后来又发现,Q_θ是可以被V_θ表示的,于是我们的函数就只需要一个神经网络计算状态价值了。
那么,A_θ^GAE 是什么呢?
累了,不想写太多数学的东西,简单说吧。GAE表示“一般优势估计”,是为了估计A_θ 在时间序列上的累积值而提出来的。所以,它是一个最后计算得到的估计值,它和我们智能体的回报相关。
PPO:什么是off- policy
PPO是off-policy的。啥是off-policy呢?
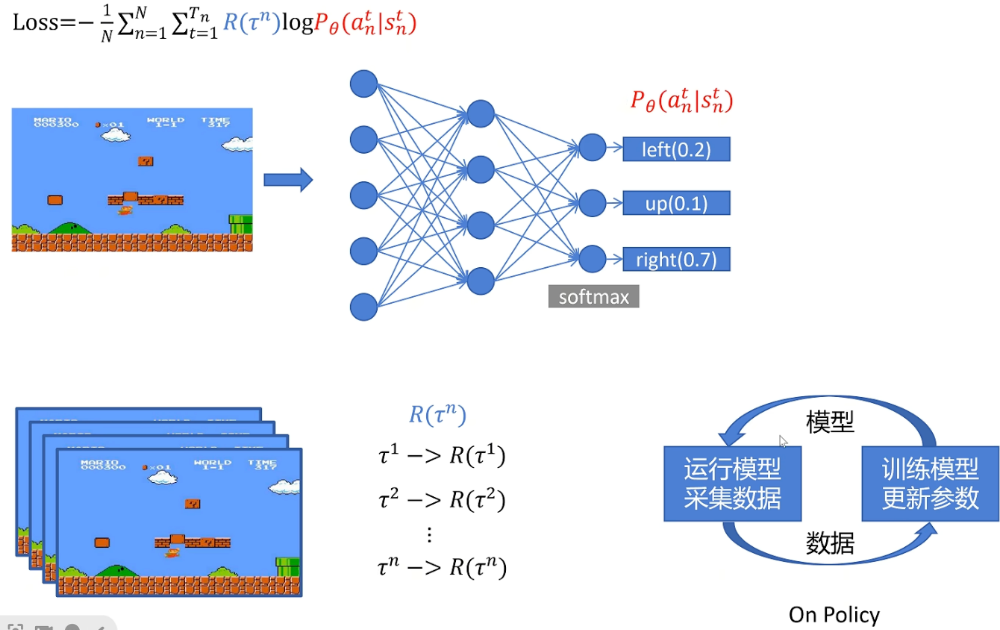
如图所示,我们传统的强化学习使用on-policy——就是智能体运行,采集到数据,然后再用这些数据更新自己的参数,如此往复。相当于是一个自己“摸爬滚打”的过程。
于是就有一个明显的缺点,那就是训练速度慢。
而on-policy是这样的:
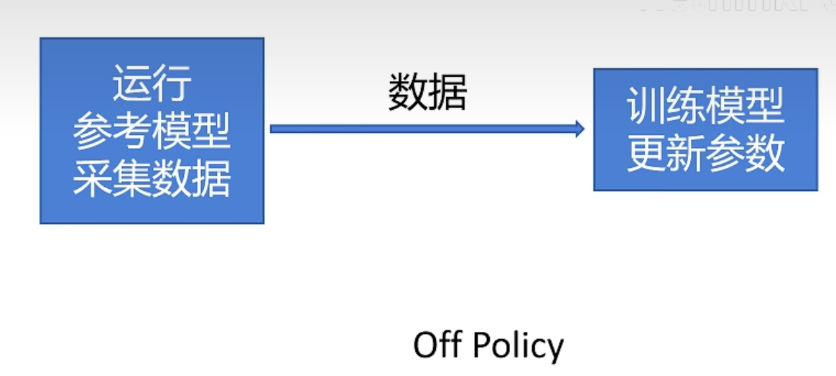
LLM的训练可以分为预训练和后训练两个阶段:
预训练:经典的“向模型投喂数据”阶段,模型通过大规模网络数据进行下一个token的预测训练;
后训练:这是我们尝试提升模型推理能力的阶段。后训练通常包括两个阶段,分别是SFT(监督式微调),目的是使得模型可以模拟专家的行为;RLHF,这个阶段的存在是因为,SFT阶段的专家数据往往不够多,于是使用RL来在有限的数据里学到更微妙的内容,相当于是对齐。
参考模型往往就是一个SFT之后的模型。那么这时候会有一个疑问,就是说,参考模型的行为和我们在新的任务场景中所需要的行为是不完全一样的呀(比如,参考模型是一个经常上课开小差的学生,而我们并不希望训练的模型有这样的行为)。
累了,问deepseek:
一、先理解 On-Policy(同策略) vs Off-Policy(异策略)
想象你在学做菜:
On-Policy:你严格按照菜谱(当前策略)做菜,并且根据这次做的结果改进菜谱。
→ 边实践边改进,但只能用自己的经验(比如 SARSA 算法)。Off-Policy:你一边看别人的做菜视频(旧策略产生的数据),一边改进自己的菜谱(新策略)。
→ 用别人的经验改进自己。
→ 核心问题:旧数据和新策略的“行为方式”不同,如何调整?
二、重要性采样(Importance Sampling)
它要解决什么问题?
假设旧策略(比如随机做菜)产生了数据,但新策略(比如精细做菜)想用这些数据学习。
问题:旧数据中的行为概率和新策略不同,直接使用会有偏差。
核心思想
给旧数据中的每个动作“打个权重”,修正概率差异,让数据适用于新策略。
→ 就像用“汇率”转换货币:旧策略的数据是“外币”,重要性采样是“汇率”,转换成新策略能用的“本币”。
三、举个具体例子 🌰
假设有两个策略:
旧策略(行为策略):随机向左或向右移动,概率各 50%。
新策略(目标策略):专家策略,向右概率 90%,向左 10%。
现在有一段旧策略产生的数据:在某个状态选择了向右,获得了奖励。
直接使用旧数据的问题
如果新策略直接学习这段数据,会忽略一个事实:
→ 旧策略中向右的概率是 50%,而新策略选择向右的概率是 90%。
→ 新策略更倾向于向右,但旧数据中的右移“参考价值”需要调整。
重要性权重计算
重要性权重 = 新策略选择动作的概率 / 旧策略选择动作的概率
在这个例子中:
重要性权重 = 0.9(新策略向右概率) / 0.5(旧策略向右概率) = 1.8
结果修正
用这个权重(1.8)乘以旧数据中的奖励,再更新新策略。
→ 相当于告诉新策略:“这段数据对你更有参考价值,因为你会更频繁向右”。
四、为什么需要重要性采样?
Off-Policy 的核心需求:用旧策略的数据训练新策略(比如用随机探索的数据训练一个精细策略)。
概率差异修正:新旧策略的动作概率不同,直接取平均会引入偏差,必须通过权重调整。
类比:考试估分
旧策略:随机答题(每题正确率 50%)。
新策略:认真答题(正确率 90%)。
如果直接用旧策略的分数评估新策略的水平,显然不公平。重要性采样就像根据新旧策略的“答题认真程度差异”,重新计算分数。
五、总结
关键公式:
重要性权重 = π_new(动作) / π_old(动作)(π_new:新策略的动作概率,π_old:旧策略的动作概率)
